观看此文应具备基础知识:学习电路至正弦激励下动态电路的稳态分析一章、微积分基础、微分方程等
约定正文符号如下:(①②③…等为公式标识符;❶❷❸…等为文末注释标识符),相关量后面的‘h’是homogeneous通解的首字母,‘p’是particular特解的首字母,数学中的虚数 i 为了避免在电路中与电流 i 混淆,所以虚数 i在此记作 j,相量法中I头上的点由于这里不好编辑,所以用头上的~表示
首先,先来看一道简单的电路习题:

题目: 如图\(Us\)为正弦电压源,其值为\(Umsin{wt+\varphi u}\),其中\(\varphi u\)是电压源的初相位。设电感初始值\(iL{0^{-} }=0\)安培,\(t=0\)时,开关S从1合向2,求换路后电感电流\(iL{t}(t≥0)\).
解1(对比之前直流电压源\(Us\)做法,这是我一开始想到的方法,但是理解到后面,我认为这个方法应该是不通的):
一阶RC/RL电路经典法求解一般步骤:
- 建立描述电路的微分方程
- 求齐次微分方程的通解和非齐次微分方程的一个特解
- 将齐次微分方程的通解与非齐次微分方程的的一个特解相加,得到非齐次微分方程的通解,利用初始条件确定通解的系数
1.描述换路后电路的微分方程为(实质为KVL):
\(L\frac{di_{L} }{dt} +Rdi_{L}=U_{m} sin{wt+\varphi u}\)----①
令\(\frac{di_{L}}{dt} =y^{'}\) ,\(iL=y\),代入①式有:
\(Ly^{'} +Ry=U_{m} sin{wt+\varphi u}\) ----②
2.列写特征方程(P算子解法❶):\(LP+R=0\Rightarrow P=-\frac{R}{L}\),
因而齐次微分方程的通解为:$yh=ke^{- t} $(其中k为待确定量),
自由项\(f{t}=U_{m} sin{wt+\varphi u}\),
设特解\(yp=A\),\(y^{'} =0\)(A为常数)代入原方程②,有
\(yp=A=\frac{U_{m} }{R}sin[wt+\varphi u] =I_{m} sin[wt+\varphi u]\),
3.方程通解为:\(y=yh+yp=i_{L}[0^{+} ]=k\cdot e^{-\frac{L}{R} \cdot t} +I_{m} sin[wt+\varphi u]\),
代入初始条件:\(y|_{t=0^{+} } =i_{L}[0^{+}] =i_{L}[0^{-}]=0\),
求得系数\(k=-I_{m} sin[wt+\varphi u]\),
最后可求得题目结果:
$i_{L}[t]=I_{m}sin[wt+u]-I_{m}sin[wt+u]e^{-t } $③(t≥0)
乍一看似乎并没有错,但这个式子应该是错误的。学过高中物理知识即可知道,电感对于交流电是有阻碍作用的(通直流阻交流),这个阻碍作用在R中并不能体现出来(因为电阻的电阻为R,也就变相说明电路中阻碍电流的只有线性电阻),而且在学习了后续课程之后可以知道,电感电容这类电学器件是有感抗与容抗的【在求解一阶动态电路三要素法中:时间常数RiC,L/Ri中Ri的含义是从电路的储能原件两端看进去的戴维南等效电阻】;
式子中的\(\varphi u\)也是错误的,学过后续课程之后也可以知道,电感上的电流是落后与电压90°相位的(同样地,电容上的电流也是超前电压90°相位的)。
所以这个方法行不通(可能有解决、改进的办法,但是我没有想出)。
解2(此为《电路原理》书中解法,有删减、补充、改动):
1.描述换路后电路的微分方程为:$L +Ri_{L}=U_{m}sin[wt+u] $----④
2.齐次微分方程的通解仍为指数形式:\(i_{Lh} =Ae^{-\frac{R}{L} \cdot t}(t≥0)\)
非齐次微分方程的一个特解与外加激励应具有同样的形式,设为:
\(i_{Lp} =I_{m} sin[wt+\varphi i ](t≥0)\)
将上式代入式子④,有:
\(wLI_{m}cos[wt+\varphi i]+RI_{m}sin[wt+\varphi i]=U_{m}sin[wt+\varphi u]\),
对等号左边进行三角变换(辅助角公式❷):
\(\sqrt{[wL]^{2} +R^{2} } \cdot I_{m} sin[wt+\varphi i+\varphi ]=U_{m} sin[wt+\varphi u]\)⑤,
其中\(\varphi\) 称为电路的阻抗角,$tan= $,
比较⑤中等号左右两边的对应项:
\(\sqrt{[wL]^{2} +R^{2} } \cdot I_{m}\Leftrightarrow U_{m}\) 与\(sin[wt+\varphi i+\varphi ]\Leftrightarrow sin[wt+\varphi u]\),
可求得:$I_{m} = \(与\)i=u-=u-arctan $,
因此,式子④的一个特解为:\(i_{Lp} =\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[wt+\varphi u-\varphi ](t≥0)\),
3.电感电流的全响应为:\(i=i_{Lh} +i_{Lp}=Ae^{-\frac{R}{L} \cdot t}+\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[wt+\varphi u-\varphi ](t≥0)\)
代入初始条件:\(i_{L} [0^{+} ]=i_{L} [0^{-} ]=0\),
有:\(A+\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[\varphi u-\varphi ]=0\Rightarrow A=-\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[\varphi u-\varphi ]\),
因此,电感电流为:
\(i_{L} =\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[wt+\varphi u-\varphi ]-\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[\varphi u-\varphi ]e^{-\frac{R}{L} \cdot t}\)⑥(t≥0).
【总结】
1.比较解1、解2结果③(现将Im按照解1变形)与⑥:
\(i_{L}[t]=\frac{U_{m} }{R} sin[wt+\varphi u]-\frac{U_{m} }{R}sin[wt+\varphi u]\cdot e^{-\frac{R}{L}t }\) ③
\(i_{L} =\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[wt+\varphi u-\varphi ]-\frac{U_{m} }{\sqrt{[wL]^{2} +R^{2} } } sin[\varphi u-\varphi ]e^{-\frac{R}{L} \cdot t}\)⑥
可见,解1后面分析是正确的:
◆sin[这里的值是有相位变换的]
◆比较分子$U_{m} \(下面的分母,可见解1中的R的确不是单纯的电路电阻值。含储能元件的此电路中对电流阻力的表现形式是这样的:\){ } $。
可预见的是:电感元件在电路中对电流阻力作用是与电源的角频率w与其本身电感值L共同决定的。这些便是接下来的感抗方面的内容了。
2.通过解2我们发现:上例仅仅是最简单的一阶动态电路,其复杂程度已经令人咂舌。
可以预见,如果在各种大型电路网络中利用此类方法求解,是比较困难的(请允许我用了“比较”这个词汇,鄙见:因为在计算机飞速发展的时代,求解一些普通点的微分方程似乎并不是什么难事?)。由此:
我们不禁想象,是不是有一种方法,可以不用求解微分方程,仅仅像之前直流电源那样,利用线性方程求解,那该多好啊?
于是,天才工程师斯泰因梅茨疯狂的在电压电流上加了个点,一个伟大的方法诞生了——相量法!
开始
我们盯住上述题目中:电压源\(U_{s}= Umsin{wt+\varphi u}\) 以及用微分方程求解电路过程中的各个方程式。其中有各种各样的已知量、未知量:电压、电流的幅值$U_{m} /I_{m} \(,初相角\)u/i\(,以及激励的频率\)w$等等。
帅的人可能已经发现:无论是题设、过程、结果,我们如此多的方程式中只要含有三角函数的式子,其中的频率无一不是\(w\)!显然,在给定频率的正弦电压电源中,其电路的频率保持不变。可以预见的,正弦电流电源同样如此。
那么,我们想:我们在题目中关注的量(也可以理解为:其中参与方程式变换的量)一般为三个:电压、电流的幅值$U_{m} /I_{m} \(;初相角\)u/i\(;激励的频率\)w\(。既然电路中自始至终频率\)w$死活不变【可以理解为:方程式中参与实际运算的量仅仅为幅值与初相角】,那么我们是不是可以残忍的抛弃这个好吃懒做的家伙、仅仅关心真正的两位劳模:幅值与初相角呢?
如何将频率*时间从三角函数的大别墅【在此将三角函数如\(sin[wt+\varphi
]\)中的[]戏称为别墅,其中的频率*时间、初相角为别墅中的成员】中拖出来扔到大街?在抛弃频率*时间这个好吃懒做的家伙之后,运算过程能否得以简化?让我们拭目以待。
常规的三角函数变换手段似乎难以将别墅中阴险的频率小伙子诱骗出来,是时候发大招了——欧拉的愤怒!
欧拉公式❸【请阅读下文之前务必阅读此注释,重要!重要!重要!】:
\(e^{jx} =cosx+j\cdot sinx\)
仔细观察公式,将之与$ Umsin{wt+u}$比较、分析。还是没有启发?
那么我们将欧拉公式进一步变换:\(e^{j[wt+\varphi ]} =cos[wt+\varphi ]+j\cdot sin[wt+\varphi ]\Rightarrow e^{jwt+j\varphi } =cos[wt+\varphi ]+j\cdot sin[wt+\varphi ]\),
再变:\(e^{jwt } \cdot e^{j\varphi } ={coswt+jsinwt ]\cdot {cos\varphi +jsin\varphi }\),现在呢,是不是有点眉目了?
我们思考:正弦电压源表达式三角函数大别墅中的两个成员不就可以运用欧拉公式变换为两个e指数函数的乘积形式,从而将之从别墅中分离吗?
按照这个思路,根据:\(k\cdot sinx=k\cdot IM[e^{jx} ]=IM[k\cdot e^{jx} ]\),
于是,电流源\(i=I_{m} sin[wt+\varphi i]\)可以表示为:\(I_{m} \cdot IM[e^{j[wt+\varphi i]} ]=IM[I_{m} \cdot e^{j[wt+\varphi i]} ]\)⑦,
高中的时候(嗯,电路原理课程前面也推到过的,在此不细说),我们就知道:正弦交流电的幅值是有效值的$ \(倍,即\)I_{m} = I$。
⑦式又可以表示为:\(IM[\sqrt{2} I\cdot e^{j\varphi i}\cdot e^{jwt} ]\)⑧,现在总算将\(IM[ e^{jwt} ]\),也就是\(wt\)这个家伙拖出来了!【——来人呐,帮朕把这个刁民拖出去,打一百二十大板!——嗻!】
再继续之前,还要介绍一个概念:旋转因子❹。
那让我们乘胜追击,单独看剩下的两个劳模(幅值与初相角):\(\sqrt{2} I\cdot e^{j\varphi i}\),乘号$$左侧代表幅值,右侧代表初相角。
那么我们之后的运算全都建立在⑧式中的两个劳模 \(I\cdot e^{j\varphi i}\),等到运算完成之后,再把\(wt\)这个家伙塞进来,反向逆推算子,不就可以得到结果了吗?
为了简便起见,我们约定:\(\tilde{I} =I\cdot e^{j\varphi i} =I\cdot ∠\varphi i\)
小结:
\(I_{m} sin[wt+\psi i]=IM[\sqrt{2}I\cdot e^{\psi i} \cdot e^{jwt} ]\),\(e^{jx} =cosx+j\cdot sinx\)

结束
1.将\(i(t)\)变成$ $的过程称为从时域到频域的相量变换: \[ i[t]=I_{m} cos[wt+\varphi ]\Rightarrow i[t]=IM[I_{m}e^{j[wt+\varphi ]} ]\Rightarrow \tilde{I} =I_{m}e^{j\varphi } \Rightarrow \tilde{I}=I_{m} \] 2.大体流程图:
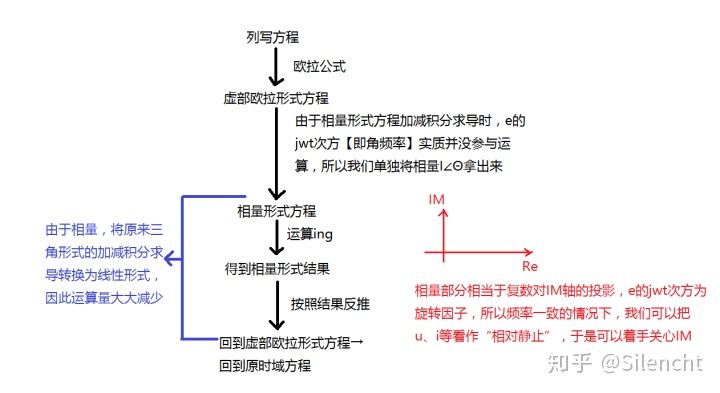
3.以下是知友【@frente nemo 】对相量法的相关理解,供参考:
我想他用的就是以不变应万变的道理吧,所有量都以一个频率在变,其效果就更想对静止差不多了吧,但是他们对电容和电感产生了新的影响,因为他们的电流电压之间有微分和积分的关系。在新的思路下你可以将电感变成jwl,将电容变成1/jwc,接下来你又改思考为什么可以这样变。这是在极坐标下的电流电压关系可以推导出来的。你要再追根溯源说,为什么可以用复数来代替正弦?那是因为欧拉公式将正弦转化成了复数表达。你还问欧拉公式又是什么?它是迈克劳林(泰勒)公式得到的。你必须不断地思考,不断地提问才能明白这一起是怎么回事。
链接:https://www.zhihu.com/question/19851763/answer/37465084
4.接下来,按照思路,可以推导“元件约束与基尔霍夫定律下的相量形式”,然后就可以求解相关习题了!~
最后引用这位知友的一句话作为本文的结束:
伟大的人类用自己的智慧把交流量头上打个点,然后一切又归于平静了。
注释
【约定注释部分符号如下:(ⅠⅡⅢ…等为公式标识符】
❶列写特征方程求解一阶微分方程(在我看来,电路求解中的P算子解法接近于高等数学微分方程的特征方程解法,三要素解法接近于高等数学中的通解公式解法。)
下面给出【高等数学一阶微分方程知识以及其特征方程解法】与【直流电压源动态电路中P算子解法】的互相对照:
高等数学一阶线性微分方程基础知识:
对于形如:
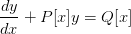
----Ⅰ的方程,叫做一阶线性微分方程。
如果对于Ⅰ中,若:
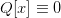
,那么方程:
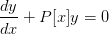
----Ⅱ称为齐次的;否则,方程Ⅰ称为非齐次的。
一阶非齐次线性微分方程特征方程解法(部分过程参考自文献):
如果一阶常系数非齐次线性微分方程的一般形式是:$my^{'} +py=qe^{x} $ (m、p、q为常数,一般情况下\(\lambda =0\))。
对于此方程,一般先求出对应的齐次方程的通解,再用常数变易法求原方程的通解。 对应的齐次方程的通解:列写对应特征方程\(mr+p=0\)(r为未知量),求解得出$r=- \(,则齐次通解为:\)yh=k e^{-x }$ ,下面求非齐次特解。 特解应设为\(yp=x^{k} \cdot e^{\lambda x} Rm[x]\),求解步骤:
\(Rm[x]\)是与q同次的多项式,因\(q\)为常数,所以\(Rm[x]\)取\(x=1\)的常数,在此我们约定为常数A
\(\lambda =0\)与r对照比较,一般情况下\(\lambda \ne r\),因此\(\lambda =0\)不是特征方程的根,所以特解表达式中k取0
把特解表达式(此时特解表达式应为\(yp =A\),\(y^{'} =0\)[常数A求导为0])代入(需要求导的求导之后代入)一般形式的原方程(此时原方程应为\(my^{'} +py=q)\),得:
\(pA=q\Rightarrow yp=A=\frac{q}{p}\)
原方程的通解等于其对应的齐次方程的通解与其一个特解的和:
\(y=yh+yp=k \cdot e^{-\frac{p}{m}x }+\frac{q}{p}\)
❷在数学中,辅助角是指三角变换中收缩变换的代表辅助角公式:\(asinx+bcosx=\sqrt{(a^2+b^2)} sin(x+\varphi )\),其中\(tan\varphi =\frac{b}{a}\)
❸欧拉公式与复数:
在介绍欧拉公式之前,先要说明的是虚数。经历过高考的我们都知道,复数这个词可以用一个形如\(a+jb\)的整体来表示,这里a、b都是通常的实数且b≠0,而\(j\)和通常实数不同,具有\(j^{2} =-1\)这个性质。虽然看起来很难理解,但是在此只能强迫读者默认这个事实。如果想对复数有更深入的认识,不妨读一下《复分析 可视化方法》这本书。
1. 复数及其运算: 设A为一复数,a和b分别是它的实部和虚部,则复数A的代数形式(又称直角坐标形式)为:\(A=a+jb\),上式中,\(j=\sqrt{-1}\) 为虚数单位。
2. 复数的实部和虚部分别用下列符号表示:\(Re[A]=a,Im[A]=b\)。在此不用纠结于Re与Im,可以看作一种算子(就像高中做的那些新定义题目一样,如:定义a#b=ab,那么我们遇到2#3就等于2×3=6)。
【但是为了防止算子\(Im\)与电流幅值\(I_{m}\) 混淆,在本文中我们约定用\(IM\)做取虚部算子写法】
复数经过它们的运算后分别得到该复数的实部和虚部。
复数A还可以表示为三角形式:\(A=|A|[cos\Theta +jsin\Theta ]\),
根据欧拉公式又可进一步写成指数形式:$A=|A|e^{j} $,
还可以改写为极坐标形式:\(A=|A|∠\Theta\) 。
其中:若$A=a+jb=|A|∠$,则 \(a=|A|cos\Theta ,b=|A|sin\Theta\) ,\(|A|=\sqrt{a^{2} +b^{2} } ,\Theta =arctan[\frac{b}{a} ]\)
几何表示:
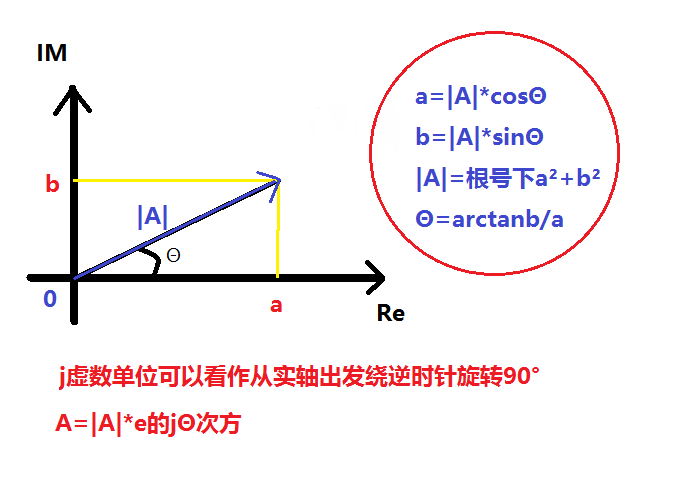
3. 复数的运算:【图片来源:《电路原理》P390-392】




文字浓缩:
- 两个复数之和A+B由通常向量加法的平行四边形法则给出
- 两个复数的乘法:AB之长是A之长与B之长的乘积,AB的幅角是A与B的幅角之和
4. 欧拉公式的猜想式推导(非严格): 设\(f(x)=\cos x+j\sin x\),有:\(f(x)f(y)=f(x+y)\), 猜知:\(f(x)\)为指数函数,设: \(f(x)=e^{kx} =\cos x+j\sin x\)(其中k为常数,j为虚数单位) 两边求导,得: \(k\cdot e^{kx} =-\sin x+j\cos x=j^{2}\sin x+j\cos x=j[\cos x+j\sin x]\), 其中[]中便是\(e^{kx}\),即:\(k\cdot e^{kx} =j\cdot e^{kx}\), 消去\(e^{kx}\)(其不为0), 则\(k=j\), 因此我们有:\(e^{jx} =\cos x+j\sin x\)
5.
更加有趣的是,在《复分析》这本书的注释中,有这样一句话:
我们相信,现在的证法支持一个观点,即这种恒等式只是复数乘法的简单法则的复杂化了的表现形式。
被誉为上帝公式的欧拉公式,仅仅是复数乘法法则的表现形式!有兴趣的可以读一读这本书的前面几章内容~
❹旋转因子:
我们假设初值:\(A=|A|\cdot e^{j\Theta }\) ,如图:

然后做运算:\(A\cdot e^{j\psi } =|A|\cdot e^{j\Theta } \cdot e^{j\psi }=|A|\cdot e^{j[\Theta +\psi ]}\) ,
我们可以想象,A的初值是A的绝对值乘e的\(j\Theta\) 次方,当它再乘e的$j$次方时,几何直观看来为:

总结为:任何一个复数乘以\(e^{j\psi }\) 之后,等于这个复数模不变,相角逆时针增加\(\psi\) 度
\(e^{jwt}\) 是以角速度w逆时针方向旋转的单位长度的有向线段,称之为旋转因子。
参考文献
- 《 一阶常系数线性微分方程的某些求法的比较》,作者:汤文菊、胡荣、简志宏 .文章编号:1008-8458(2005)04-0009-02
- 《高等数学》第七版上册,同济大学数学系编,高等教育出版社,2015年6月第五次印刷
- 《电路原理》编著:于歆杰、朱桂萍、陆文娟,清华大学出版社,2007年3月第一次印刷
- 《工程电路分析》(engineering circuit analysis)第七版,作者:【美】William H. Hayt,Jr. Jack E.Kemmerly Steven M.Durbin 编著 ,周玲玲、蒋乐天 等译.,电子工业出版社,2007年7月第一次印刷
- 《复分析 可视化方法》(visual complex analysis)作者:【美】Tristan Needhan 著,齐民友译,人民邮电出版社,2009年7月北京第一次印刷